Return to site
Return to site

Qr Householder Method

broken image


This article will discuss QR Decomposition in Python. In previous articles we have looked at LU Decomposition in Python and Cholesky Decomposition in Python as two alternative matrix decomposition methods. QR Decomposition is widely used in quantitative finance as the basis for the solution of the linear least squares problem, which itself is used for statistical regression analysis.

One of the key benefits of using QR Decomposition over other methods for solving linear least squares is that it is more numerically stable, albeit at the expense of being slower to execute. Hence if you are performing a large quantity of regressions as part of a trading backtest, for instance, you will need to consider very extensively whether QR Decomposition is the best fit (excuse the pun).

Typically this approach to QR is performed using Householder or Givens transformations. As discussed in the next section, another method for producing the QR decomposition, and a far more transparent method for producing an orthonormal basis, uses the Gram-Schmidt (G-S) algorithm. Harville (1997) points out that the QR decomposition is unique. This paper) that the Gaussian-elimination and Householder methods for upper-triangularization are on the order of n3. Thus, these methods are far more efficient than naive cofactor expansion. 1.3 Computation of matrix inverses In elementary linear algebra, we are taught to compute inverses using cofactor expansion. Don't watch this video!New (and better quality) videos about the Householder Transformation can be found in this playlist: https://www.youtube.com/playlist. Another algorithm for determining the QR Q R decomposition of a matrix which requires fewer operations and is less susceptible to rounding error is the method of Householder reflectors. The method depends upon the following theorem.

For a square matrix $A$ the QR Decomposition converts $A$ into the product of an orthogonal matrix $Q$ (i.e. $Q^TQ=I$) and an upper triangular matrix $R$. Hence:

begin{eqnarray*} A = QR end{eqnarray*}

There are a few different algorithms for calculating the matrices $Q$ and $R$. We will outline the method of Householder Reflections, which is known to be more numerically stable the the alternative Gramm-Schmidt method. I've outlined the Householder Reflections method below.

Note, the following explanation is an expansion of the extremely detailed article on QR Decomposition using Householder Reflections over at Wikipedia.

A Householder Reflection is a linear transformation that enables a vector to be reflected through a plane or hyperplane. Essentially, we use this method because we want to create an upper triangular matrix, $R$. The householder reflection is able to carry out this vector reflection such that all but one of the coordinates disappears. The matrix $Q$ will be built up as a sequence of matrix multiplications that eliminate each coordinate in turn, up to the rank of the matrix $A$.

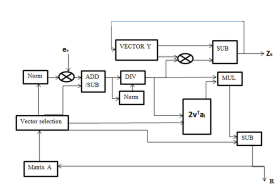
The first step is to create the vector $mathbb{x}$, which is the $k$-th column of the matrix $A$, for step $k$. We define $alpha = -sgn(mathbb{x}_k)(||mathbb{x}||)$. The norm $||cdot||$ used here is the Euclidean norm. Given the first column vector of the identity matrix, $I$ of equal size to $A$, $mathbb{e}_1 = (1,0,...,0)^T$, we create the vector $mathbb{u}$:

begin{eqnarray*} mathbb{u} = mathbb{x} + alpha mathbb{e}_1 end{eqnarray*}

Once we have the vector $mathbb{u}$, we need to convert it to a unit vector, which we denote as $mathbb{v}$:

begin{eqnarray*} mathbb{v} = mathbb{u}/||mathbb{u}|| end{eqnarray*}

Now we form the matrix $Q$ out of the identity matrix $I$ and the vector multiplication of $mathbb{v}$:

begin{eqnarray*} Q = I - 2 mathbb{v} mathbb{v}^T end{eqnarray*}

$Q$ is now an $mtimes m$ Householder matrix, with $Qmathbb{x} = left( alpha, 0, ..., 0right)^T$. We will use $Q$ to transform $A$ to upper triangular form, giving us the matrix $R$. We denote $Q$ as $Q_k$ and, since $k=1$ in this first step, we have $Q_1$ as our first Householder matrix. We multiply this with $A$ to give us:

begin{eqnarray*} Q_1A = begin{bmatrix} alpha_1&star&dots&star 0 & & & vdots & & A' & 0 & & & end{bmatrix} end{eqnarray*}

The whole process is now repeated for the minor matrix $A'$, which will give a second Householder matrix $Q'_2$. Now we have to 'pad out' this minor matrix with elements from the identity matrix such that we can consistently multiply the Householder matrices together. Hence, we define $Q_k$ as the block matrix:

begin{eqnarray*} Q_k = begin{pmatrix} I_{k-1} & 0 0 & Q_k'end{pmatrix} end{eqnarray*}

Qr Householder Method Name

Once we have carried out $t$ iterations of this process we have $R$ as an upper triangular matrix:

begin{eqnarray*} R = Q_t ... Q_2 Q_1 A end{eqnarray*}

$Q$ is then fully defined as the multiplication of the transposes of each $Q_k$:

begin{eqnarray*} Q = Q^T_1 Q^T_2 ... Q^T_t end{eqnarray*}
Householder transform
Householder

This gives $A=QR$, the QR Decomposition of $A$.

To calculate the QR Decomposition of a matrix $A$ with NumPy/SciPy, we can make use of the built-in linalg library via the linalg.qr function. This is significantly more efficient than using a pure Python implementation:

The output of the QR decomposition includes $A$, $Q$ and $R$. As a basic sanity check we can see that $R$ is in fact an upper triangular matrix:

You aren't likely to ever need a pure Python implementation of QR Decomposition (homework notwithstanding), but I feel that it is helpful to gain an understanding of the Householder Reflections algorithm, so I have written my own implementation:

The output from the Householder method implemented in pure Python is given below:

You can see that we get the same answers as above in the SciPy implementation, albeit with a few more significant figures! One has to be extremely careful in numerical algorithms when dealing with floating point arithmetic, but that is a discussion for another day.

Method

$initialize$So far, we have only shown existence , but How do we compute QR decompositions?

Householder Reflections

Householder reflection is $H=I-2vv'$ where $norm v2=1$ which reflects over hyperplane orthogonal to $v$

Lemma. Householder reflections are orthogonal matrices

Proof. $~$ HOMEWORK

We use a series of Householder reflections to reduce $APi$ to an upper triangular matrix, and the resultant product of Householder matrices gives us $Q,$, i.e. $$underbrace{H_rcdots H_1}_{Q'}APi=R$$

Qr Householder Method

First, find $H_1$ that makes every entry below $R_{11}$ zero,
begin{align*}
H_1a_1&=R_{11}e_1
R_{11}e_1&=a_1-2v_1v_1'a_1
v_1(underbrace{2v_1'a_1}_text{scalar})&=a_1-R_{11}e_1
implies~v_1&=frac{a_1-R_{11}e_1}{norm{a_1-R_{11}e_1}2}
implies~R_{11}e_1&=pmnorm{a_1}2
v_1&=frac{a_1-norm{a_1}{}e_1}{norm{vphantom{big|};!a_1-norm{a_1}{}e_1}2}
implies H_1&=I-frac{(a_1-norm{a_1}{}e_1)(a_1-norm{a_1}{}e_1)'}{norm{vphantom{big|};!a_1-norm{a_1}{}e_1}{}_2^2}
end{align*}

Then, we have
$$H_aAPi~=~defhmatres{{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!mat{&&&tilde{A}_2&&&}end{matrix}end{matrix}}}left[{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!underbrace{mat{&&&tilde{A}_2&&&}}_text{repeat on these}end{matrix}end{matrix}}^{vphantom{Big|}}right]$$

Givens Rotations

Givens rotations $Gij$ where $Gij$ is the identity matrix except
- $Gij_{ii}=Gij_{jj}=lambda$
- $Gij_{ij}=sigma$
- $Gij_{ji}=-sigma$

$$text{for example, },G^{(2,4)}=mat{1&0&0&00&lambda&0&sigma0&0&1&00&-sigma&0&lambda}$$

HOMEWORK $~$ Show that Givens rotation is orthogonal when $sigma^2+lambda^2=1$

We can also use Givens rotations to compute the decomposition, so that $$underbrace{G_Tcdots G_1}_{Q'}APi=R$$

To find $G_1$, we look for a Givens rotation $G^{(1,2)}$ that will make the entry in row 2 column 1 of the product equal to zero. Consider the product with the following matrix $M$ $$mat{lambda&sigma-sigma&lambda},mat{M_{11}&M_{12}&cdots&M_{1m}M_{21}&M_{22}&cdots&M_{2m}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=mat{hphantom{-}lambda M_{11}+sigma M_{21}&hphantom{-1}lambda M_{12}+sigma M_{22}&cdots&hphantom{-1}lambda M_{1m}+sigma M_{2m}-sigma M_{11}+lambda M_{21}&-sigma M_{12}+lambda M_{22}&cdots&-sigma M_{1m}+lambda M_{2m}}$$

To find $G_1$, we solve $$begin{matrix}begin{split}-sigma M_{11}+lambda M_{21}&=0text{s.t. }~~~~~~~~~~~~~sigma^2+lambda^2&=1end{split}end{matrix}~~~~~~~implies~~~~~~~begin{matrix}lambda=frac{M_{11}}{sqrt{M_{11}^2+M_{21}^2}}~~~text{and}~~~sigma=frac{M_{21}}{sqrt{M_{11}^2+M_{21}^2}}end{matrix}$$

Example

Householder Qr Matlab

Now, we can repeat this process to successively make all entries below the diagonal zero, giving us a QR decomposition.

Qr Householder Method

This gives $A=QR$, the QR Decomposition of $A$.

To calculate the QR Decomposition of a matrix $A$ with NumPy/SciPy, we can make use of the built-in linalg library via the linalg.qr function. This is significantly more efficient than using a pure Python implementation:

The output of the QR decomposition includes $A$, $Q$ and $R$. As a basic sanity check we can see that $R$ is in fact an upper triangular matrix:

You aren't likely to ever need a pure Python implementation of QR Decomposition (homework notwithstanding), but I feel that it is helpful to gain an understanding of the Householder Reflections algorithm, so I have written my own implementation:

The output from the Householder method implemented in pure Python is given below:

You can see that we get the same answers as above in the SciPy implementation, albeit with a few more significant figures! One has to be extremely careful in numerical algorithms when dealing with floating point arithmetic, but that is a discussion for another day.

$initialize$So far, we have only shown existence , but How do we compute QR decompositions?

Householder Reflections

Householder reflection is $H=I-2vv'$ where $norm v2=1$ which reflects over hyperplane orthogonal to $v$

Lemma. Householder reflections are orthogonal matrices

Proof. $~$ HOMEWORK

We use a series of Householder reflections to reduce $APi$ to an upper triangular matrix, and the resultant product of Householder matrices gives us $Q,$, i.e. $$underbrace{H_rcdots H_1}_{Q'}APi=R$$

Qr Householder Method

First, find $H_1$ that makes every entry below $R_{11}$ zero,
begin{align*}
H_1a_1&=R_{11}e_1
R_{11}e_1&=a_1-2v_1v_1'a_1
v_1(underbrace{2v_1'a_1}_text{scalar})&=a_1-R_{11}e_1
implies~v_1&=frac{a_1-R_{11}e_1}{norm{a_1-R_{11}e_1}2}
implies~R_{11}e_1&=pmnorm{a_1}2
v_1&=frac{a_1-norm{a_1}{}e_1}{norm{vphantom{big|};!a_1-norm{a_1}{}e_1}2}
implies H_1&=I-frac{(a_1-norm{a_1}{}e_1)(a_1-norm{a_1}{}e_1)'}{norm{vphantom{big|};!a_1-norm{a_1}{}e_1}{}_2^2}
end{align*}

Then, we have
$$H_aAPi~=~defhmatres{{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!mat{&&&tilde{A}_2&&&}end{matrix}end{matrix}}}left[{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!underbrace{mat{&&&tilde{A}_2&&&}}_text{repeat on these}end{matrix}end{matrix}}^{vphantom{Big|}}right]$$

Givens Rotations

Givens rotations $Gij$ where $Gij$ is the identity matrix except
- $Gij_{ii}=Gij_{jj}=lambda$
- $Gij_{ij}=sigma$
- $Gij_{ji}=-sigma$

$$text{for example, },G^{(2,4)}=mat{1&0&0&00&lambda&0&sigma0&0&1&00&-sigma&0&lambda}$$

HOMEWORK $~$ Show that Givens rotation is orthogonal when $sigma^2+lambda^2=1$

We can also use Givens rotations to compute the decomposition, so that $$underbrace{G_Tcdots G_1}_{Q'}APi=R$$

To find $G_1$, we look for a Givens rotation $G^{(1,2)}$ that will make the entry in row 2 column 1 of the product equal to zero. Consider the product with the following matrix $M$ $$mat{lambda&sigma-sigma&lambda},mat{M_{11}&M_{12}&cdots&M_{1m}M_{21}&M_{22}&cdots&M_{2m}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=mat{hphantom{-}lambda M_{11}+sigma M_{21}&hphantom{-1}lambda M_{12}+sigma M_{22}&cdots&hphantom{-1}lambda M_{1m}+sigma M_{2m}-sigma M_{11}+lambda M_{21}&-sigma M_{12}+lambda M_{22}&cdots&-sigma M_{1m}+lambda M_{2m}}$$

To find $G_1$, we solve $$begin{matrix}begin{split}-sigma M_{11}+lambda M_{21}&=0text{s.t. }~~~~~~~~~~~~~sigma^2+lambda^2&=1end{split}end{matrix}~~~~~~~implies~~~~~~~begin{matrix}lambda=frac{M_{11}}{sqrt{M_{11}^2+M_{21}^2}}~~~text{and}~~~sigma=frac{M_{21}}{sqrt{M_{11}^2+M_{21}^2}}end{matrix}$$

Householder Qr Matlab

Now, we can repeat this process to successively make all entries below the diagonal zero, giving us a QR decomposition.

HOMEWORK

  1. Determine the computational complexity for QR decomposition using
    • Gram-Schmidt
    • Modified Gram-Schmidt
    • Householder reflections
    • Givens rotations
  2. Compare the complexity of Householder vs Givens for a sparse matrix
  3. Implement QR decomposition using Householder reflections, (input matrix A of full column rank and output Q,R)
  4. Repeat 3 using Givens rotations

$$~$$

'Large' data least squares

$AinRnm$, where $ngg m~~$ (which is a different situation than $mgg n$)

Optional reference : 'Incremental QR Decomposition' , by Gentleman.

We can apply QR decomposition to solving the least squares equation $Ax=b$ since
begin{align*}
hat{x}&=(A'A)inv A'b
&=((QR)'(QR))inv(QR)'b
&=(R'cancel{Q'Q}R)inv R'Q'b
&=(R'R)inv R'Q'b
&=Rinvcancel{(R')inv R'}Q'b
&=Rinv Q'b
end{align*}

Qr Householder Method Validation

We need to find $Rinv$ and $Q'b$. To do so, consider just the first $m!+!1$ rows of the matrix $mat{A&b},$ and perform QR decomposition to get $$mat{tilde{R}&tilde{Q}'tilde{b}0&tilde{s}}$$ Then, we add one row at a time to the bottom and perform Givens rotations so that $$mat{tilde{R}&tilde{Q}'tilde{b}0&tilde{s}a_{m+2}&b_{m+2}}~~~implies~~~mat{tilde{R}_{m+2}&tilde{Q}_{m+2}'tilde{b}_{m+2}0&tilde{s}_{m+2}0&0}$$

Qr Householder Method Tutorial

$$~$$

Householder Matrix





broken image
PreviousNext
Cookie Use
We use cookies to improve browsing experience, security, and data collection. By accepting, you agree to the use of cookies for advertising and analytics. You can change your cookie settings at any time. Learn More
Accept all
Settings
Decline All
Cookie Settings
Necessary Cookies
These cookies enable core functionality such as security, network management, and accessibility. These cookies can’t be switched off.
Analytics Cookies
These cookies help us better understand how visitors interact with our website and help us discover errors.
Preferences Cookies
These cookies allow the website to remember choices you've made to provide enhanced functionality and personalization.
Save